Table of Contents

• 1. Introduction
• 2. A Conceptual Understanding of Promises
  • Interlude: The Girl Who Hated Queues
  • 2.1. What Are Promises?
  • Interlude: Order of Execution
  • 2.2. Promises and Concurrency
  • Interlude: Abstracting Over Expressions
• 3. Understanding the Promises Machinery
  • 3.1. Sequencing Expressions with Promises
  • 3.2. A Minimal Promise Implementation
• 4. Promises and Error Handling
  • Interlude: When Computations Fail
  • 4.1. Handling Errors With Promises
  • 4.2. Failure Propagation With Promises
• 5. Combining Promises
  • 5.1. Combining Promises Deterministically
  • 5.2. Combining Promises Non-Deterministically
• 6. A Practical Understanding of Promises
  • 6.1. Introducing ECMAScript Promises
  • 6.2. A Closer Look Into .then
• 7. When Are Promises A Bad Fit?
• 8. Conclusion
• References
• Additional Resources
• Promise Libraries
• Changelog

1. Introduction

Most implementations of JavaScript happen to be single-threaded, and given the language’s semantics, people tend to use callbacks to direct concurrent processes. While there isn’t anything particularly wrong with using Continuation-Passing Style in JavaScript, in practice it’s very easy for them to make the code harder to read, and more procedural than it should be.

Many solutions for this have been proposed, and the usage of promises to synchronise these concurrent processes is one of them. In this blog post we’ll look at what promises are, how they work, and why you should or shouldn’t use them.

Note This article assumes the reader is at least familiar with higher-order functions, closures, and callbacks (continuation-passing style). You might still be able to get something out of this article without that knowledge, but it’s better to come back after acquiring a basic understanding of those concepts.

2. A Conceptual Understanding of Promises

Let’s start from the beginning and answer a very important question: “What are promises anyway?”

To answer this question, we’ll consider a very common scenario in real life.

Interlude: The Girl Who Hated Queues

Girfriends trying to have dinner at a very popular food place.

Alissa P. Hacker and her girlfriend decided to have dinner at a very popular restaurant. Unfortunately, as it was to be expected, when they arrived there all of the tables were already occupied.

In some places, this would mean that they would either have to give up and choose somewhere else to eat, or wait in a long queue until they could get a table. But Alissa hated queues, and this place had the perfect solution for her.

“This is a magical device that represents your future table…”

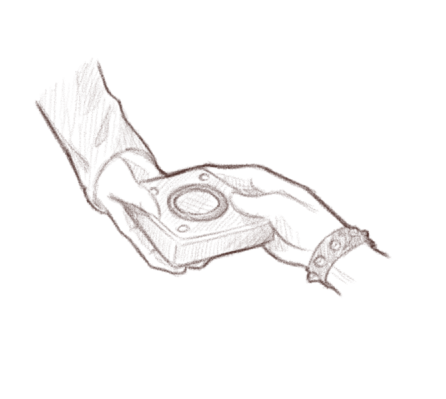A device that represents your future table in the restaurant.

“Worry not, my dear, just hold on to this device, and everything will be taken care of for you,” the lady at the restaurant said, as she held a small box.

“What is this…?” Alissa’s girlfriend, Rue Bae, asked.

“This is a magical device that represents your future table at this restaurant,” the lady spoke, then beckoned to Bae. “There’s no magic, actually, but it’ll tell you when your table is ready so you can come and eat,” she whispered.

2.1. What Are Promises?

Much like the “magical” device that stands in for your future table at the restaurant, promises exist to represent something that will be available in the future. In a programming language, these things are values.

Whole apple in, apple slices out.

In the synchronous world, it’s very simple to understand computations when thinking about functions: you put things into a function, and the function gives you something in return.

This input-goes-in-output-comes-out model is very simple to understand, and something most programmers are very familiar with. All syntactic structures and built-in functionality in JavaScript assume that your functions will follow this model.

There is one big problem with this model, however: in order for us to be able to get our delicious things out when we put things into the function, we need to sit there and wait until the function is done with its work. But ideally we would want to do as many things as we can with the time we have, rather than sit around waiting.

To solve this problem promises propose that, instead of waiting for the value we want, we get something that represents that value right away. We can then move on with our lives, and, at some later point in time, come back to get the value we need.

Promises are representations of eventual values.

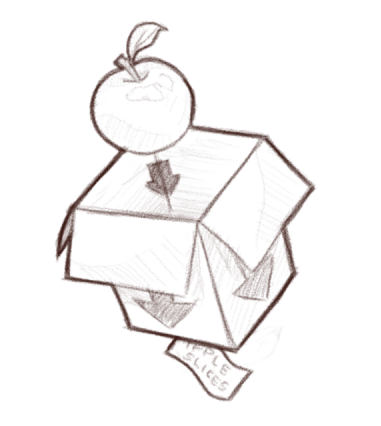Whole apple in, ticket for rescuing our delicious apple slices later out.

Interlude: Order of Execution

Now that we, hopefully, understand what a promise is, we can look at how promises help us write concurrent programs in an easier way. But before we do that, let’s take a step back and think about a more fundamental problem: the order of execution of our programs.

As a JavaScript programmer you might have noticed that your program executes in a very peculiar order, which happens to be the order in which you write the instructions in your program’s source code:

var circleArea = 10 * 10 * Math.PI;
var squareArea = 20 * 20;

If we execute this program, first our JavaScript VM will run the computation for circleArea, and once it’s finished, it’ll execute the computation for squareArea. In other words, our programs are telling the machines “Do this. Then do that. Then do that. Then…”

Question time! Why must our machine execute circleArea before squareArea? Would there be any issues if we inverted the order, or executed both at the same time?

Turns out, executing everything in order is very expensive. If circleArea takes too long to finish, then we’re blocking squareArea from executing at all until then. In fact, for this example, it doesn’t matter which order we pick, the result is always going to be the same. The order expressed in our programs is too arbitrary.

[…] order is very expensive.

We want our computers to be able to do more things, and do more things faster. To do so, let’s, at first, dispense with order of execution entirely. That is, we’ll assume that in our programs all expressions are executed at the exact same time.

This idea works very well with our previous example. But it breaks as soon as we try something slightly different:

var radius = 10;
var circleArea = radius * radius * Math.PI;
var squareArea = 20 * 20;
print(circleArea);

If we don’t have any order at all, how can we compose values coming from other expressions? Well, we can’t, since there’s no guarantee that the value would have been computed by the time we need it.

Let’s try something different. The only order in our programs will be defined by the dependencies between the components of the expressions. Which, in essence, means that expressions are executed as soon as all of its components are ready, even if other things are already executing.

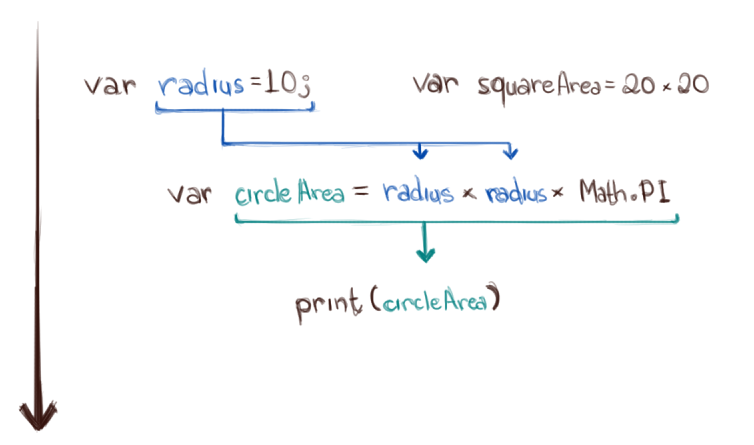The dependency graph for our simple example.

Instead of having to declare which order the program should use when executing, we’ve only defined how each computation depends on each other. With that data in hand, a computer can create the dependency graph above, and figure out itself the most efficient way of executing this program.

Fun fact! The graph above describes very well how programs are evaluated in the Haskell programming language, but it’s also very close to how expressions are evaluated in more well-known systems, such as Excel.

2.2. Promises and Concurrency

The execution model described in the previous section, where order is defined simply by the dependencies between each expression, is very powerful and efficient, but how do we apply it to JavaScript?

We can’t apply this model directly to JavaScript because the language semantics are inherently synchronous and sequential. But we can create a separate mechanism to describe dependencies between expressions, and to resolve these dependencies for us, executing the program according to those rules. One way to do this is by introducing this concept of dependencies on top of promises.

This new formulation of promises consists of two major components: Something that makes representations of values, and can put values in this representation. And something that creates a dependency between one expression and a value, creating a new promise for the result of the expression.

Creating representations of future values. 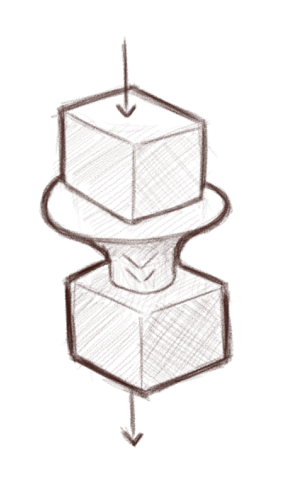Creating dependencies between values and expressions.

Our promises represent values that we haven’t computed yet. This representation is opaque: we can’t see the value, nor interact with the value directly. Furthermore, in JavaScript promises, we also can’t extract the value from the representation. Once you put something in a JavaScript promise, you cannot take it out of the promise ¹.

This by itself isn’t much useful, because we need to be able to use these values somehow. And if we can’t extract the values from the representation, we need to figure out a different way of using them. Turns out that the simplest way of solving this “extraction problem” is by describing how we want our program to execute, by explicitly providing the dependencies, and then solving this dependency graph to execute it.

For this to work, we need a way of plugging the actual value in the expression, and delaying the execution of this expression until strictly needed. Fortunately JavaScript has got our back in this: first-class functions serve exactly this purpose.

Interlude: Abstracting Over Expressions

If one has an expression of the form a + 1, then it is possible to abstract over this expression such that a becomes a value that can be plugged in, once it’s ready. This way, the expression:

var a = 2;
a + 1;
// { replace `a` by its current value }
// => 2 + 1
// { reduce the expression }
// => 3

Becomes the following lambda abstraction²:

var abstraction = function(a) {
  return a + 1;
};

// We can then plug `a` in:
abstraction(2);
// => (a => a + 1)(2)
// { replace `a` by the provided value }
// => (2 => 2 + 1)
// { reduce the expression }
// => 2 + 1
// { reduce the expression }
// => 3

First-class functions are a very powerful concept (whether they are anonymous — a lambda abstraction — or not). Since JavaScript has them we can describe these dependencies in a very natural way, by transforming the expressions that use the values of promises into first-class functions so we can plug in the value later.

3. Understanding the Promises Machinery

3.1. Sequencing Expressions with Promises

Now that we went through the conceptual nature of promises, we can start understanding how they work in a machine. We’ll describe the operations used to create promises, put values in them, and describe the dependencies between expressions and values. For the sake of our examples we’ll use the following very descriptive operations, which happen to be used by no existing Promises implementation:

• createPromise() constructs a representation of a value. The value must be provided at later point in time.

• fulfil(promise, value) puts a value in the promise, allowing the expressions that depend on the value to be computed.

• depend(promise, expression) defines a dependency between the expression and the value of the promise. It returns a new promise for the result of the expression, so new expressions can depend on that value.

Let’s go back to the circles and squares example. For now, we’ll start with the simpler one: turning the synchronous squareArea into a concurrent description of the program by using promises. squareArea is simpler because it only depends on the side value:

// The expression:
var side = 10;
var squareArea = side * side;
print(squareArea);

// Becomes:
var squareAreaAbstraction = function(side) {
  var result = createPromise();
  fulfil(result, side * side);
  return result;
};
var printAbstraction = function(squareArea) {
  var result = createPromise();
  fulfil(result, print(squareArea));
  return result;
}

var sidePromise = createPromise();
var squareAreaPromise = depend(sidePromise, squareAreaAbstraction);
var printPromise = depend(squareAreaPromise, printAbstraction);

fulfil(sidePromise, 10);

This is a lot of noise, if we compare with the synchronous version of the code, however this new version isn’t tied to JavaScript’s order of execution. Instead, the only constraints on its execution are the dependencies we’ve described.

3.2. A Minimal Promise Implementation

There’s one open question left to be answered: how do we actually run the code so the order follows from the dependencies we’ve described? If we’re not following JavaScript’s execution order, something else has to provide the execution order we want.

Luckily, this is easily definable in terms of the functions we’ve used. First we must decide how to represent values and their dependencies. The most natural way of doing this is by adding this data to the value returned from createPromise.

First, Promises of something must be able to represent that value, however they don’t necessarily contain a value at all times. A value is only placed into the promise when we invoke fulfil. A minimal representation for this would be:

data Promise of something = {
  value :: something | null
}

A Promise of something springs into existence containing the value null. At some later point in time someone may invoke the fulfil function for that promise, and from there on the promise will contain the given fulfilment value. Since promises can only be fulfilled once, that value is what the promise will contain for the rest of the program.

Given that it’s not possible to figure out if a promise has already been fulfilled by just looking at the value (null is a valid value), we also need to keep track of the state the promise is in, so we don’t risk fulfilling it more than once. This requires a small change to the our previous representation:

data Promise of something = {
  value :: something | null,
  state :: "pending" | "fulfilled"
}

We also need to handle the dependencies that are created by the depend function. A dependency is a function that will, eventually, be filled with the value in the promise, so it can be evaluated. One promise can have many functions which depend on its value, so a minimal representation for this would be:

data Promise of something = {
  value :: something | null,
  state :: "pending" | "fulfilled",
  dependencies :: [something -> Promise of something_else]
}

Now that we’ve decided on a representation for our promises, let’s start by defining the function that creates new promises:

function createPromise() {
  return {
    // A promise starts containing no value,
    value: null,
    // with a "pending" state, so it can be fulfilled later,
    state: "pending",
    // and it has no dependencies yet.
    dependencies: []
  };
}

Since we’ve decided on our simple representation, constructing a new object for that representation is fairly straightforward. Let’s move to something more complicated: attaching dependencies to a promise.

One of the ways of solving this problem would be to put all of the dependencies created in the dependencies field of the promise, then feed the promise to an interpreter that would run the computations as needed. With this implementation, no dependency would ever execute before the interpreter is started. We’ll not implement promises this way because it doesn’t fit how people usually write JavaScript programs³.

Another way of solving this problem comes from the realisation that we only really need to keep track of the dependencies for a promise while the promise is in the pending state, because once a promise is fulfilled we can just execute the function right away!

function depend(promise, expression) {
  // We need to return a promise that will contain the value of
  // the expression, when we're able to compute the expression
  var result = createPromise();

  // If we can't execute the expression yet, put it in the list of
  // dependencies for the future value
  if (promise.state === "pending") {
    promise.dependencies.push(function(value) {
      // We're interested in the eventual value of the expression
      // so we can put that value in our result promise.
      depend(expression(value), function(newValue) {
        fulfil(result, newValue);
        // We return an empty promise because `depend` requires one promise
        return createPromise();
      })
    });

  // Otherwise just execute the expression, we've got the value
  // to plug in ready!
  } else {
    depend(expression(promise.value), function(newValue) {
      fulfil(result, newValue);
      // We return an empty promise because `depend` requires one promise
      return createPromise();
    })
  }

  return result;
}

The depend function takes care of executing our dependent expressions when the value they’re waiting for is ready, but if we attach the dependency too soon that function will just end up in an array in the promise object, so our job is not done yet. For the second part of the execution, we need to run the dependencies when we’ve got the value. Luckily, the fulfil function can be used for this.

We can fulfil promises that are in the pending state by calling the fulfil function with the value we want to put in the promise. This is a good time to invoke any dependencies that were created before the value of the promise was available, and takes care of the other half of the execution.

function fulfil(promise, value) {
  if (promise.state !== "pending") {
    throw new Error("Trying to fulfil an already fulfilled promise!");
  } else {
    promise.state = "fulfilled";
    promise.value = value;
    // Dependencies may add other dependencies to this promise, so we
    // need to clean up the dependency list and copy it so our
    // iteration isn't affected by that.
    var dependencies = promise.dependencies;
    promise.dependencies = [];
    dependencies.forEach(function(expression) {
      expression(value);
    });
  }
}

4. Promises and Error Handling

Interlude: When Computations Fail

Not all computations can always produce a valid value. Some functions, like a / b, or a[0] are partial, and thus only defined for a subset of possible values for a or b. If we write programs that contain partial functions, and we hit one of the cases that the function can’t handle, we won’t be able to continue executing the program. In other words, our entire program would crash.

A better way of incorporating partial functions in a program is by making it total. That is, defining the parts of the function that weren’t defined before. In general, this means that we consider the cases the function can handle a form of “Success”, and the cases it can’t handle a form of “Failure”. This alone already allows us to write entire programs that may continue executing even when faced with a computation that can’t produce a valid value:

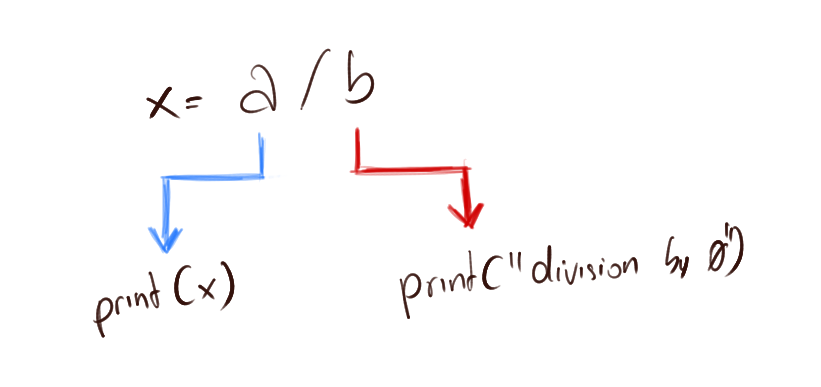Branching on partial functions

Branching on each possible failure is a reasonable way of handling them, but not necessarily a practical one. For example, if we compose three computations that could fail, that means we’d have to define at least 6 different branches, for the simplest composition!

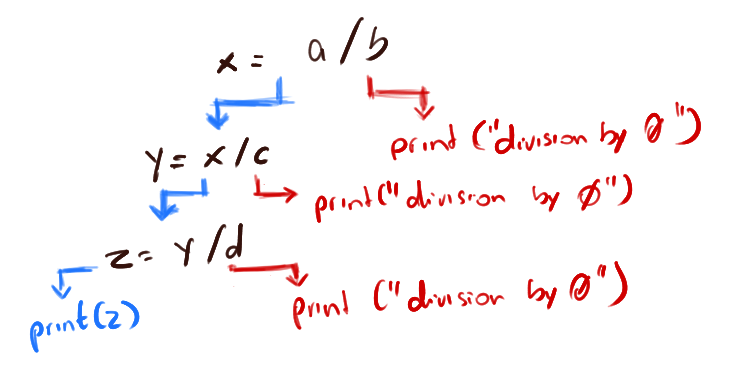Branching on every partial function

Fun fact! Some programming languages, like OCaml, prefer this style of error handling because it’s very explicit on what’s happening. In general functional programming favours explicitness, but some functional languages, like Haskell, use an interface called Monad⁴ to make error handling (among other things) more practical.

Ideally, we’d like to write just y / (x / (a / b)), and handle possible errors just once, for the entire composition, rather than handling errors in each sub-expression. Programming languages have different ways of letting you do this. Some let you ignore errors entirely, or at least put off touching it as much as possible, like C and Go. Some will let the program crash, but give you tools to recover from the crashing, like Erlang. But the most common approach is to assign a “failure handler” to a block of code where failures may happen. JavaScript allows the latter approach through the try/catch statement, for example.

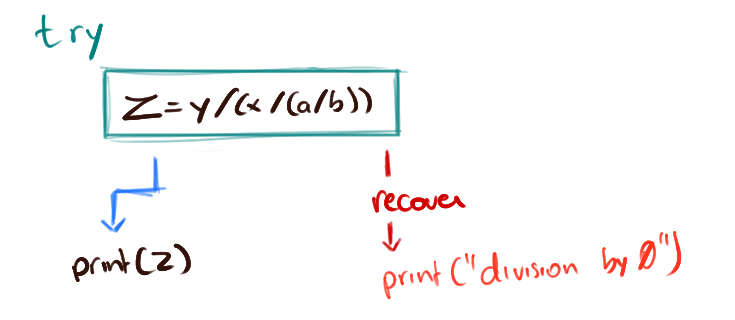One of the approaches for handling failures in a practical way

4.1. Handling Errors With Promises

Our formulation of Promises so far does not admit failures. So, all of the computations that happen in promises must always produce a valid result. This is a problem if we were to run a computation like a / b inside a promise, because if b is 0, like in 2 / 0, that computation can’t produce a valid result.

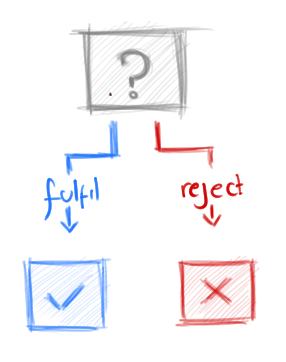Possible states of our new promise

We can modify our promise to contemplate the representation of failures quite easily. Currently our promises start at the pending state, and then it can only be fulfilled. If we add a new state, rejected, then we can model partial functions in our promises. A computation that succeeds would start at pending, and eventually move to fulfilled. A computation that fails would start at pending, and eventually move to rejected.

Since we now have the possibility of failure, the computations that depend on the value of the promise also must be aware of that. For now we’ll have our depend failure just take an expression to run when the promise is fulfilled, and one expression to run when the promise is rejected.

With this, our new representation of promises becomes:

data Promise of (value, error) = {
  value :: value | error | null,
  state :: "pending" | "fulfilled" | "rejected",
  dependencies :: [{
    fulfilled :: value -> Promise of new_value,
    rejected  :: error -> Promise of new_error
  }]
}

The promise may contain either a proper value, or an error, and contains null until it settles (is either fulfilled or rejected). To handle this, our dependencies also need to know what to do for proper values and error values, so the array of dependencies has to be changed slightly.

Besides the change in representation, we need to change our depend function, which now reads like this:

// Note that we now take two expressions, rather than one.
function depend(promise, onSuccess, onFailure) {
  var result = createPromise();

  if (promise.state === "pending") {
    // Dependencies now gets an object containing
    // what to do in case the promise succeeds, and
    // what to do in case the promise fails. The functions
    // are roughly the same as the previous ones.
    promise.dependencies.push({
      fulfilled: function(value) {
        depend(onSuccess(value),
               function(newValue) {
                 fulfil(result, newValue);
                 return createPromise()
               },
               // We have to care about errors that
               // happen when applying the expression too
               function(newError) {
                 reject(result, newError);
                 return createPromise();
               });
      },

      // The rejected branch does the same as the
      // fulfilled branch, but uses the onFailure
      // expression.
      rejected: function(error) {
        depend(onFailure(error),
               function(newValue) {
                 fulfil(result, newValue);
                 return createPromise();
               },
               function(newError) {
                 reject(result, newError);
                 return createPromise();
               });
        }
      });
    }
  } else {
    // if the promise has been fulfilled, we run onSuccess
    if (promise.state === "fulfilled") {
      depend(onSuccess(promise.value),
             function(newValue) {
               fulfil(result, newValue);
               return createPromise();
             },
             function(newError) {
               reject(result, newError);
               return createPromise();
             });
    } else if (promise.state === "rejected") {
      depend(onFailure(promise.value),
             function(newValue) {
               fulfil(result, newValue);
               return createPromise();
             },
             function(newError) {
               reject(result, newError);
               return createPromise();
             });
    }
  }

  return result;
}

And finally, we need a way of putting errors in promises. For this we need a reject function.:

function reject(promise, error) {
  if (promise.state !== "pending") {
    throw new Error("Trying to reject a non-pending promise!");
  } else {
    promise.state = "rejected";
    promise.value = error;
    var dependencies = promise.dependencies;
    promise.dependencies = [];
    dependencies.forEach(function(pattern) {
      pattern.rejected(error);
    });
  }
}

We also need to review the fulfil function slightly due to our change to the dependencies field:

function fulfil(promise, value) {
  if (promise.state !== "pending") {
    throw new Error("Trying to fulfil a non-pending promise!");
  } else {
    promise.state = "fulfilled";
    promise.value = value;
    var dependencies = promise.dependencies;
    promise.dependencies = [];
    dependencies.forEach(function(pattern) {
      pattern.fulfilled(value);
    });
  }
}

And with these new additions, we’re ready to start putting computations that may fail in our promises:

// A computation that may fail
var div = function(a, b) {
  var result = createPromise();

  if (b === 0) {
    reject(result, new Error("Division By 0"));
  } else {
    fulfil(result, a / b);
  }

  return result;
}

var printFailure = function(error) {
  console.error(error);
};

var a = 1, b = 2, c = 0, d = 3;
var xPromise = div(a, b);
var yPromise = depend(xPromise,
                      function(x) {
                        return div(x, c)
                      },
                      printFailure);
var zPromise = depend(yPromise,
                      function(y) {
                        return div(y, d)
                      },
                      printFailure);

4.2. Failure Propagation With Promises

The last code example will never execute zPromise, because c is 0, and it causes the computation div(x, c) to fail. This is exactly what we expect, but right now we need to pass the failure branch every time we define a computation in our promise. Ideally, we’d like to only define the failure branches where necessary, like we do with try/catch for synchronous computations.

Turns out it’s trivial for our promise to support this functionality. It’s only necessary to define our branches for success and failure all the time if we can’t abstract over it, and it’s often the case with control flow. For example, in JavaScript, it’s not possible to abstract over an if statement, or a for statement, because they’re second-class control flow mechanisms, and you can’t modify those, pass them around, or store them in variables. Our promises are first-class objects, they have a concrete representation of failures and successes, which we can inspect and react to whenever we want, not just at the point they are created.

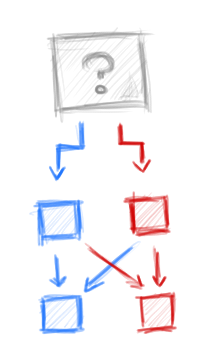Possible lifecycle of a promise chain

In order to be able to achieve something similar to try/catch we first must be able to do two things with our representation of successes and failures:

• recover from a failure: If a computation failed, I must be able to turn that value into some sort of success that makes sense. This allows, for example, the use of a default value when retrieving some data from a Map or Array structure. map.get("foo").recover(1) + 2 would give you 3 if there’s no "foo" key in the map.

• fail anytime: If I have a successful computation, I must be able to turn that value into a failure, and if I have a failure, I must be able to keep the failure. The former allows short-circuiting a computation, and the latter allows failure propagation. With both, you’re able to capture the semantics of (a / b) / (c / d) failing entirely if any subexpression fails.

Luckily for us, the depend function already does most of this work. Because depend requires its expressions to return whole promises it’s able to propagate not only the values, but the state the promise is in. This is important since if we define just a successful branch, and the promise fails, we want to propagate not only the value, but also its failure state.

With these mechanisms already in place, supporting simple failure propagation, error handling, and short-circuiting on failures requires adding two operations: chain, which creates a dependency on the successful value of a promise, but short-circuits on failures; and recover, which creates a dependency on the failure value of a promise, and allows recovering from that error.

function chain(promise, expression) {
  return depend(promise, expression,
                function(error) {
                  // We propagate the state and
                  // value of the error by just
                  // creating an equivalent promise
                  var result = createPromise();
                  reject(result, error);
                  return result;
                })
}

function recover(promise, expression) {
  return depend(promise,
                function(value) {
                  // We propagate successful values
                  // by just creating an equivalent
                  // promise.
                  var result = createPromise();
                  fulfil(result, value);
                  return result;
                },
                expression)
}

We can then use these two functions to simplify our previous division example:

var a = 1, b = 2, c = 0, d = 3;
var xPromise = div(a, b);
var yPromise = chain(xPromise, function(x) {
                                 return div(x, c)
                               });
var zPromise = chain(yPromise, function(y) {
                                 return div(y, d);
                               });
var resultPromise = recover(zPromise, printFailure);

5. Combining Promises

5.1. Combining Promises Deterministically

While sequencing operations with promises requires one to create a chain of dependencies, combining promises concurrently just requires that the promises don’t have a dependency on each other.

For our Circle example we have a computation that is naturally concurrent. The radius expression and the Math.PI expression don’t depend on each other, so they can be computed separately, but circleArea depends on both. In terms of code, we have the following:

var radius = 10;
var circleArea = radius * radius * Math.PI;
print(circleArea);

If one wanted to express this with promises, they’d have:

var circleAreaAbstraction = function(radius, pi) {
  var result = createPromise();
  fulfil(result, radius * radius * pi);
  return result;
};

var printAbstraction = function(circleArea) {
  var result = createPromise();
  fulfil(result, print(circleArea));
  return result;
};

var radiusPromise = createPromise();
var piPromise = createPromise();

var circleAreaPromise = ???;
var printPromise = chain(circleAreaPromise, printAbstraction);

fulfil(radiusPromise, 10);
fulfil(piPromise, Math.PI);

We have a small problem here: circleAreaAbstraction is an expression that depends on two values, but depend is only able to define dependencies for expressions that depend on a single value!

There are a few ways of working around this limitation, we’ll start with the simple one. If depend can provide a single value for one expression, then it must be possible to capture the value in a closure, and extract the values from the promises one at a time. This does create some implicit ordering, but it shouldn’t impact concurrency too much.

function wait2(promiseA, promiseB, expression) {
  // We extract the value from promiseA first.
  return chain(promiseA, function(a) {
    // Then we extract the value of promiseB
    return chain(promiseB, function(b) {
      // Now that we've got access to both values,
      // we can execute the expression that depends
      // on more than one value:
      var result = createPromise();
      fulfil(result, expression(a, b));
      return result;
    })
  })
}

With this, we can define circleAreaPromise as the following:

var circleAreaPromise = wait2(radiusPromise, piPromise, circleAreaAbstraction);

We could define wait3 for expressions that depend on three values, wait4 for expressions that depend on four values, and so on, and so forth. But wait* creates an implicit ordering (promises are executed in a particular order), and it requires that we know the amount of values that we’re going to plug in advance. So it doesn’t work if we want to wait for an entire array of promises, for example (although one could combine wait2 and Array.prototype.reduce for that).

Another way of solving this problem is to accept an array of promises, and execute each one as soon as possible, then give back a promise for an array of the values the original promises contained. This approach is a little more complicated, since we need to implement a simple Finite State Machine, but there is no implicit ordering (besides JavaScript’s own execution semantics).

function waitAll(promises) {
  // An array of the values of the promise, which we'll fill in
  // incrementally.
  var values = new Array(promises.length);
  // How many promises we're still waiting for
  var pending = values.length;
  // The resulting promise
  var result = createPromise();
  // Whether the promise has been resolved or not
  var resolved = false;

  // We start by executing each promise. We keep track of the
  // original index so we know where to put the value in the 
  // resulting array.
  promises.forEach(function(promise, index) {
    // For each promise, we'll wait for the promise to resolve,
    // and then store the value in the `values` array.
    depend(promise, function(value) {
      if (!resolved) {
        values[index] = value;
        pending = pending - 1;

        // If we finished waiting for all of the promises, we
        // can put the array of values in the resulting promise
        if (pending === 0) {
          resolved = true;
          fulfil(result, values);
        }
      }
      // We don't care about doing anything else with this promise.
      // We return an empty promise because `depends` requires it.
      return createPromise();
    }, function(error) {
      if (!resolved) {
        resolved = true;
        reject(result, error);
      }
      return createPromise();
    })
  });

  // Finally, we return a promise for the eventual array of values
  return result;
}

If we were to use waitAll for the circleAreaAbstraction, it would look like the following:

var circleAreaPromise = chain(waitAll([radiusPromise, piPromise]),
                              function(xs) {
                                return circleAreaAbstraction(xs[0], xs[1]);
                              })

5.2. Combining Promises Non-Deterministically

We’ve seen how to combine promises, but so far we can only combine them deterministically. This doesn’t help us if we need to, for example, select the fastest of two computations. Maybe we’re searching for something on two servers, and we don’t care which one answers, we’ll just go with the fastest one.

In order to support this we’ll introduce some non-determinism. In particular, we need an operation that, given two promises, takes the value and state of the one which resolves the fastest. The idea behind the operation is simple: run two promises concurrently, and wait for the first resolution, then propagate that to the resulting promise. The implementation is somewhat less simple, since we need to keep state around:

function race(left, right) {
  // Create the resulting promise.
  var result = createPromise();

  // Waits for both promises concurrently. doFulfil
  // and doReject will propagate the result/state of
  // the first promise to resolve. This is done by
  // checking the current state of `result` to make
  // sure it's already pending.
  depend(left, doFulfil, doReject);
  depend(right, doFulfil, doReject);

  // Return the resulting promise
  return result;

  
  function doFulfil(value) {
    if (result.state === "pending") {
      fulfil(result, value);
    }
  }

  function doReject(value) {
    if (result.state === "pending") {
      reject(result, value);
    }
  }
}

With this we can start combining operations by choosing between them non-deterministically. If we take the previous example:

function searchA() {
  var result = createPromise();
  setTimeout(function() {
    fulfil(result, 10);
  }, 300);
  return result;
}

function searchB() {
  var result = createPromise();
  setTimeout(function() {
    fulfil(result, 30);
  }, 200);
  return result;
}

var valuePromise = race(searchA(), searchB());
// => valuePromise will eventually be 30

Choosing between more than two promises is possible, because race(a, b) basically becomes a or b depending on which one resolves the fastest. So if we have race(c, race(a, b)), and b resolves first, then that’s the same as race(c, b). Of course, typing race(a, race(b, race(c, ...))) isn’t the best thing, so we can write a simple combinator to do that for us:

function raceAll(promises) {
  return promises.reduce(race, createPromise());
}

And then we can use it:

raceAll([searchA(), searchB(), waitAll([searchA(), searchB()])]);

Another way of choosing between two promises non-deterministically is to wait for the first one to be successfully fulfilled. For example, if you’re trying to find a valid download link in a list of mirrors, you don’t want to fail if the first one fails, you want to download from the first mirror you can, and fail if all of them fail. We can write an attempt operation to capture this:

function attempt(left, right) {
  // Creates the resulting promise.
  var result = createPromise();

  // doFulfil will propagate the result/state of the first
  // promise that resolves successfully, whereas doReject
  // will aggregate the errors until all of the promises
  // fail.
  //
  // We need to keep track of the errors that happened
  var errors = {}

  // Now we can wait for both promises, just like in `race`.
  // The difference here is that `doReject` needs to know
  // which promise it is rejecting, to keep track of the
  // errors.
  depend(left, doFulfil, doReject('left'));
  depend(right, doFulfil, doReject('right'));

  // Finally, return the resulting promise.
  return result;

  function doFulfil(value) {
    if (result.state === "pending") {
      fulfil(result, value);
    }
  }

  function doReject(field) {
    return function(value) {
      if (result.state === "pending") {
        // If we're still pending, we can safely keep aggregating
        // the errors. We make sure the error we got goes into the
        // right field of the object aggregating these errors
        errors[field] = value;

        // If we've managed to catch all of the errors, we can
        // reject the resulting promise. We reject it with all
        // of the errors that happened, in the right order.
        if ('left' in errors && 'right' in errors) {
          reject(result, [errors.left, errors.right]);
        }
      }
    }
  }  
}

Usage is the same as race, so attempt(searchA(), searchB()) would return the first promise that resolves successfully, rather than just the first promise to resolve. However, unlike race, attempt doesn’t compose naturally because it aggregates the errors. So, if we want to attempt several promises, we need to account for that:

function attemptAll(promises) {
  // Since we aggregate all promises, we need to start from a
  // rejected one, otherwise attempt would never finish if we
  // have errors.
  var initial = createPromise();
  reject(initial, []);

  // Finally, we use `attempt` to combine the promises, taking
  // care of flattening the arrays of errors at each step:
  return promises.reduce(function(result, promise) {
    return recover(attempt(result, promise), function(errors) {
      return errors[0].concat([errors[1]]);
    });
  }, createPromise());
}

attemptAll([searchA(), searchB(), searchC(), searchD()]);

6. A Practical Understanding of Promises

ECMAScript 2015 defines the concept of Promises for JavaScript, but up until now we’ve been using a very simple, but unconventional implementation of promises. The reason for this is that ECMAScript’s standard promise is too complex, and it would make it harder to explain the concepts from the ground up. However, now that you know what promises are, and how each aspect of them can be implemented, it’s very trivial to make the move to the standard promises.

6.1. Introducing ECMAScript Promises

The new version of the ECMAScript language defines a standard for promises in JavaScript. This standard differs from the minimal promise implementation we’ve introduced in a few ways, which makes it more complex, but also more practical and easier to use. The table below lists the differences between each implementation:

The main methods in the standard promise are new Promise(...), which introduce a promise object, and .then(...) which transforms it. There are a few differences in the way they work, when compared to the operations described so far.

new Promise(f) introduces a new promise object, it does so by taking a computation which eventually either succeeds or fails with a particular value. The act of succeeding and failing is captured by the two function arguments passed to the function f, which it expects. Thus:

var p = createPromise();
fulfil(p, 10);

// Becomes:
var p = new Promise((fulfil, reject) => fulfil(10));


// ---
// And:
var q = createPromise();
reject(q, 20);

// Becomes:
var p = new Promise((fulfil, reject) => reject(20));

promise.then(f, g) is an operation that creates a dependency between an expression with a hole for a value, and the value in the promise, similar to the depend operation. Both f and g are optional arguments, if they aren’t provided the promise will propagate the value in that state.

Unlike our depend, .then is a complex operation, which tries to make using promises easier. The function arguments passed to .then can return either a promise, or a regular value, in which case the operation takes care of automatically putting them into a promise for you. Thus:

depend(promise, function(value) {
  var q = createPromise();
  fulfil(q, value + 1);
  return q;
})


// ---
// Becomes:
promise.then(value => value + 1);

These allow the code using promises to be concise and easier to read, compared to our previous formulation:

var squareAreaAbstraction = function(side) {
  var result = createPromise();
  fulfil(result, side * side);
  return result;
};
var printAbstraction = function(squareArea) {
  var result = createPromise();
  fulfil(result, print(squareArea));
  return result;
}

var sidePromise = createPromise();
var squareAreaPromise = depend(sidePromise, squareAreaAbstraction);
var printPromise = depend(squareAreaPromise, printAbstraction);

fulfil(sidePromise, 10);


// ---
// Becomes
var sideP = Promise.resolve(10);
var squareAreaP = sideP.then(side => side * side);
squareAreaP.then(area => print(area));

// Which is more akin to the synchronous version:
var side = 10;
var squareArea = side * side;
print(squareArea);

Depending on multiple values concurrently is handled by the Promise.all operation, which is similar to our waitAll operation:

var radius = 10;
var pi = Math.PI;
var circleArea = radius * radius * pi;
print(circleArea);


// ---
// Becomes:
var radiusP = Promise.resolve(10);
var piP = Promise.resolve(Math.PI);
var circleAreaP = Promise.all([radiusP, piP])
                         .then(([radius, pi]) => radius * radius * pi);
circleAreaP.then(circleArea => print(circleArea));

Error and success propagation is handled by the .then operation itself, and the .catch operation is provided as a concise way of invoking .then without defining a success branch:

var div = function(a, b) {
  var result = createPromise();

  if (b === 0) {
    reject(result, new Error("Division By 0"));
  } else {
    fulfil(result, a / b);
  }

  return result;
}

var a = 1, b = 2, c = 0, d = 3;
var xPromise = div(a, b);
var yPromise = chain(xPromise, function(x) {
                                 return div(x, c)
                               });
var zPromise = chain(yPromise, function(y) {
                                 return div(y, d);
                               });
var resultPromise = recover(zPromise, printFailure);


// ---
// Becomes:
var div = function(a, b) {
  return new Promise((fulfil, reject) => {
    if (b === 0)  reject(new Error("Division by 0"));
    else          fulfil(a / b);
  })
}

var a = 1, b = 2, c = 0, d = 3;
var xP = div(a, b);
var yP = xP.then(x => div(x, c));
var zP = yP.then(y => div(y, d));
var resultP = zP.catch(printFailure);

6.2. A Closer Look Into .then

There are a few things that make the .then method different from our previous depend function. While .then is one method to define dependency relationships between eventual values and some computation, it also tries to make the usage of the method easy for the majority of cases. This makes .then a complex method⁵, but we can understand it by relating our previous machinery to this new method.

.then automatically lifts regular values

Our depend function worked in the domain of promises. It expected its dependent computation to return a promise in order to return a promise itself. .then doesn’t have this requirement. If the dependent computation returns a regular value, like 42, .then will convert that value to a promise containing the value. In essence, .then lifts regular values into the domain of promises, as needed.

Compare the simplified types of our depend function:

depend : (Promise of α, (α -> Promise of β)) -> Promise of β

With the simplified types of the .then method:

promise.then : (this: Promise of α, (α -> β)) -> Promise of β
promise.then : (this: Promise of α, (α -> Promise of β)) -> Promise of β

While in the depend function the only thing we can do is return a promise of something (and have that same something be in the resulting promise), the .then function also accepts returning a regular value, without wrapping it in a promise, for convenience.

.then disallows nested promises

Another way in which ECMAScript 2015 promises try to make usage easier for the common use cases is by disallowing nested promises. It does so by assimilating anything that has a .then method, which can be problematic in cases where you’re not expecting assimilation⁶, but otherwise relieves one from thinking about matching the types of the return values.

It’s not possible to give the .then method a sensible type in non-dependent type systems because of this feature, but, roughly, this means that the following example:

Promise.resolve(1).then(x => Promise.resolve(Promise.resolve(x + 1)))

Is equivalent to:

Promise.resolve(1).then(x => Promise.resolve(x + 1))

This is also enforced with Promise.resolve, but not with Promise.reject.

.then reifies exceptions

If an exception happens synchronously during the evaluation of a dependent computation attached through the .then method, that exception will be caught and reified as a rejected promise. In essence, this means that all of the computations attached to a promise’s values through the .then method should be treated as if implicitly wrapped in a try/catch block, such that:

Promise.resolve(1).then(x => null());

Is equivalent to:

Promise.resolve(1).then(x => {
  try {
    return null();
  } catch (error) {
    return Promise.reject(error);
  }
});

Native implementations of promises will track these and report the ones that are not handled. There’s no specification about what constitutes a “caught error” in a promise, so development tools will differ on how they report it. Chrome’s development tools, for example, will output all instances of rejected promises to the console, which might give you false positives.

.then invokes dependencies asynchronously

While our previous implementation of promises invokes the dependent computations synchronously, standard ECMAScript promises do so asynchronously. This makes it very hard for one to depend on the value of a promise without using the proper means to do so: the .then method.

Thus, the following code would not work:

var value;
Promise.resolve(1).then(x => value = x);
console.log(value);
// => undefined
// (`value = x` happens here, after all other code has finished)

This ensures that dependent computations always execute on an empty stack, though such guarantees are less essential in ECMAScript 2015, which requires that all implementations support proper tail calls⁷.

7. When Are Promises A Bad Fit?

While promises work nicely as a concurrency primitive, they are neither as general as Continuation-Passing Style, nor are they the best primitive for all use cases. Promises are placeholders for values that will eventually be computed, so they can only make sense in contexts where you would use those values themselves.

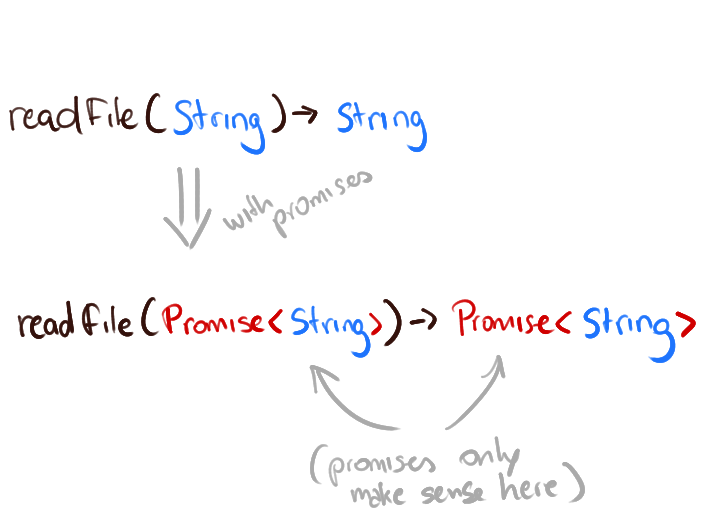Promises only make sense in the value context

Trying to use promises for anything besides that is going to result in very complicated codebases that are hard to maintain, understand, and extend. The following are some examples where promises should be entirely avoided:

• Notifying the progress of computing a particular value. Promises are used in the same context as the value itself, so just like we can’t know the progress of computing a particular string, given the string itself, we can’t do that for promises. Because of this, if you’re interested in knowing how much of a file has been downloaded, you’ll want a separate thing, like Events.

• Producing multiple values over time. Promises can only represent a single eventual value. For the cases where several values might be produced over time (the equivalent of asynchronous iterators), one would need something like Streams, Observables, or CSP Channels.

• Representing actions. This also means that it’s not possible to execute promises in order, since once one has got a promise, the computation that provides the value for it has already started. For actions you can use CPS, a Continuation monad, or a Task (co)monad, like C♯ does.

8. Conclusion

Promises are a great way of dealing with eventual values, allowing one to compose and synchronise processes that depend on values that are computed asynchronously. And while the ECMAScript 2015 standard for promises has its own set of issues, like automatically reifying errors that should crash the process, it’s a decent enough tool to deal with the aforementioned problem. Whether you use them or not, an understanding of what they are and how they work is essential, now that they’re going to be even more pervasive in the all ECMAScript projects.

References

ECMAScript® 2015 Language Specification

Allen Wirfs-Brock — Defines the standard for Promises in JavaScript.

Alice Through The Looking Glass

Andreas Rossberg, Didier Le Botlan, Guido Tack, Thorsten Brunklaus, and Gert Smolka — Presents the Alice language, which supports concurrency through futures and promises.

Haskell 98 Language and Libraries

Simon Peyton Jones — Describes, informally, the semantics of the Haskell programming language.

Communicating Sequential Processes

C. A. R. Hoare — Describes concurrent combinations of processes, such as deterministic and non-deterministic choices.

Monads For Functional Programming

Philip Wadler — Describes, amongst other things, how monads can be used for error handling in functional languages. Promise’s sequencing and error handling is very similar to the monadic formulation, although Promises don’t implement the monad interface in the ECMAScript 2015 standard.

Additional Resources

Source Code For This Blog Post

Contains all of the (commented) source code for this blog post (including a minimal implementation of promises conforming to the ECMAScript 2015 specification).

Promises/A+ Considered Harmful

Quildreen Motta — Discusses some of the problems that the Promises/A+ and the ECMAScript 2015 Promises standard have, in terms of complexity, error handling, and performance.

Professor Frisby’s Mostly Adequate Guide to Functional Programming

Brian Lonsdorf — An introductory book to functional programming in JavaScript.

Callbacks Are Imperative, Promises Are Functional: Node’s Biggest Missed Opportunity

James Coglan — Contrasts Continuation-Passing Style and Promise for describing a program’s order of execution.

Simple Made Easy

Rich Hickey — While not directly related to promises, Rich’s talk discusses “simple” and “easy” in the context of design, which is always relevant to programming.

Proper Tail Calls in Harmony

Dave Herman — Discusses the benefits of having Proper Tail Calls in ECMAScript.

Your Mouse is a Database

Erik Meijer — Discusses the coordination and orchestration of event-based and asynchronous computations in Rx using the concept of Observables.

Stream Handbook

James Halliday (substack) — Covers the basics of writing Node.js programs with Streams.

By Example: Continuation-Passing Style in JavaScript

Matt Might — Describes how continuation-passing style can be used for handling non-blocking computations in JavaScript.

The Continuation Monad

Gabriel Gonzalez — Discusses the concept of continuations as monads, in the context of the Haskell programming language.

Pause ‘n’ Play: Asynchronous C♯ Explained

Claudio Russo — Explains how asynchronous computations work in C♯ using the Task comonad, and how that solution relates to other models.

Promise Libraries

es6-promise

A polyfill for ECMAScript 2015 standard promises, for platforms that don’t implement ES2015.

Bluebird

An efficient Promises/A+ implementation.

Changelog

• 30th March, 2016: Fixes the usage example of wait2, which takes a combining function, and the signature of waitAll, which does not take a function argument, as pointed out by Martin Colwell.

Footnotes